principles-of-communication-010203

Info

本人本科主攻深度学习和计算机视觉，研究生预计的研究方向为AI for Wireless Communication，但对于通信系统的基础知识了解甚少。

目前打算阅读流程为《通信原理》（第七版）by 樊昌信 -> Digital communications 5th by John G. Proakis -> Wireless communications by Andrea Goldsmith -> Fundamentals of Wireless Communication by Tse -> Machine Learning and Wireless Communications by Eldar。本文为《通信原理》的阅读笔记，对应《通信原理》（第七版）by 樊昌信的第一、二、三章。

1. 通信基础

通信的基本概念以及通信系统的分类过于简单，这里不再赘述。

1.1. 通信系统模型

通信系统一般分为模拟系统和数字系统两类，其中数字系统为现代通信技术的主流， 于模拟系统相比其优势为：

• 抗干扰能力强
• 传输差错可控
• 便于现代数字信号处理技术对于数字信息的处理
• 易于集成
• 易于加密性处理

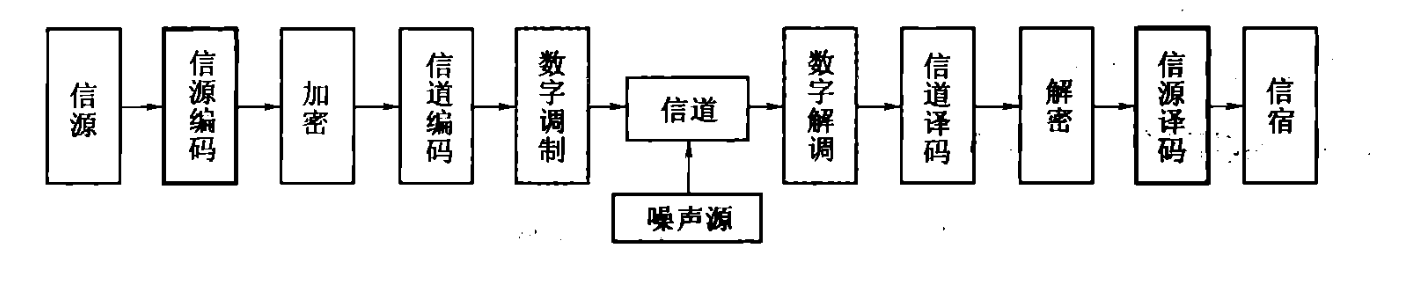
数字系统的一般模型如下图所示：

其中信源编码(Source Coding)用于完成数模AD转换并且使用压缩编码设法减少码元速率，信道编码(Channel Coding)用于增加冗余信息以增加信道传输的可靠性。同步(Synchronization)用于保证接收端的时钟与发送端的时钟同步。

1.2. 通信系统性能指标

1.2.1. 信息量

信息量是对消息发生概率的度量，其公式为$I(x)=\sum_{i=1}^{n}p(x_i)log_2\frac{1}{p(x_i)}$，其中$p(x_i)$为消息$x_i$发生的概率。

1.2.2. 有效性

对于数字系统其频带利用率定义为单位带宽内的传输速率：

$$\eta = \frac{R_B}{B} \quad (Baud/hz)$$

或

$$\eta_b = \frac{R_b}{B} \quad (bit/s/Hz)$$

其中$R_B$为码元传输速率，为单位时间内传输的码元数量，又称波特率。
对于一个$M$进制码元，其携带的比特数为$log_2M$，因此有：

$$R_b = R_B \cdot log_2M$$

1.2.3. 可靠性

数字系统通过差错概率来衡量可靠性：
误码率$P_e$是指错误接码元数所占的比率：

$$P_e = \frac{\text{错误码元数}}{\text{传输总码元数}}$$

误比特率（误信率）$P_b$是指错误比特数所占的比率：

$$P_b = \frac{\text{错误比特数}}{\text{传输总比特数}}$$

在二进制中有$P_b=P_e$

2. 确知信号

2.1. 信号的分类

关于傅里叶变换或者傅里叶级数的知识这里不再赘述，比较有意思的是，与其他书籍把信号分为离散非离散、周期非周期，樊昌信老师把信号分为两类：

• 能量信号：其能量等于一个有限值，但是平均功率为0；
• 功率信号：其能量为无穷大，但是平均功率为有限值。
  此分类方法对于随机信号也适用。

2.2. 能量信号

对于能量信号，其傅里叶变换后的频谱密度(frequency spectrum density)为：

$$S(f)=\int_{-\infty}^{\infty}x(t)e^{-j2\pi ft}dt \quad (V/Hz)$$

能量信号$s(t)$的自相关函数定义为：

$$R(\tau)=\int_{-\infty}^{\infty}s(t)s(t-\tau)dt \quad -\infty<\tau<\infty$$

该能量信号的能量为：

$$E= \int_{-\infty}^{\infty}s^2(t)dt$$

由帕塞瓦尔(Parceval)定理可知：

$$E=\int_{-\infty}^{\infty}s^2(t)dt = \int_{-\infty}^{\infty}|S(f)|^2df$$

其中$G(f)=|S(f)|^2$为能量谱密度,单位为$J/Hz$。
省去证明这里直接写结论，对于能量信号的自相关函数$R(\tau)$和能量谱密度$G(f)$构成一对傅里叶变换对：

$$R(\tau) = \int_{-\infty}^{\infty}|S(f)|^2e^{j2\pi f\tau}df$$

2.3. 功率信号

功率信号的公式以及结论与能量信号类似，其在定义自相关函数和功率谱密度都需要额外除以一个时间$T$。
对于周期性的功率信号，其频谱(freqency spectrum)为：

$$\begin{aligned} s(t) &= \sum_{n=-\infty}^{\infty}C_ne^{j2\pi f_nt} \\ C_n &= \frac{1}{T}\int_{T}s(t)e^{-j2\pi f_nt}dt \quad (V) \end{aligned}$$

要将周其函数展开为上述所示，需满足狄利克雷(Dirichlet)条件。对于物理可实现的实信号来说，其频谱函数的正频率和相应的负频率存在共轭对称关系。若将频谱函数中的负频率和正频率相应的相加，可以得出负频率只在数学上有意义，在物理上并不存在负频率。

功率信号的自相关函数定义为：

$$R(\tau) = \lim_{T\to\infty}\frac{1}{T}\int_{T}s(t)s(t-\tau)dt$$

根据功率信号在长度为$T$的区间内的能量可求得，该的功率谱密度为：

$$P(f) = \lim_{T\to\infty}\frac{1}{T}|S(f)|^2 \quad (W/Hz)$$

与能量信号类似，功率信号的自相关函数$R(\tau)$和功率谱密度$P(f)$构成一对傅里叶变换对：

$$R(\tau) = \int_{-\infty}^{\infty}P(f)e^{j2\pi f\tau}df$$

3. 随机过程

3.1. 随机过程基础

随及过程可以由两个维度进行理解：

• 横向看，随机过程就是所有样本的集合
• 纵向看，随机过程就是不同时刻下的随机变量

随机过程也可以用于数字特征比如均值、方差、自相关函数等来描述，这里不再赘述。

3.1.1. 平稳随机过程

对于平稳随机过程，其统计特性不随时间变化：

• 严平稳：对于任意时刻$t_1,t_2,t_3$，其联合概率分布相同，即：

$$f_n(x_1,x_2,\cdots,x_n;t_1,t_2,\cdots,t_n)\\=f_n(x_1,x_2,\cdots,x_n;t_1+\Delta,t_2+\Delta,\cdots,t_n+\Delta)$$

• 广义平稳随机过程，满足均值与时间无关，自相关函数只与时间差$\tau$有关：

$$\begin{aligned} E[\xi(t)]&=\int_{-\infty}^\infty xf(x)\mathrm{d}x=\mu\\ R(t_1,t_2)&=E[\xi(t_1)\xi(t_1+\tau)]=R(\tau) \end{aligned}$$

3.1.2. 各态历经性

对于随机过程，其时间平均为：

$$\begin{cases} \overline{a}=\overline{x(t)}=\lim_{T\to\infty}\frac1T\int_{-T/2}^{T/2}x(t)\mathrm{d}t\\ \overline{R(\tau)}=\overline{x(t)x(t+\tau)}=\lim_{T\to\infty}\frac1T\int_{-T/2}^{T/2}x(t)x(t+\tau)\mathrm{d}t \end{cases}$$

如果如果时间平均等于其统计平均，则具有各态历经性：

$$\begin{cases} \overline{a}=a\\ R(\tau)=\overline{R(\tau)} \end{cases}$$

3.1.3. 自相关函数和功率谱密度

对于平稳的随机过程，其自相关上述已经提到为：

$$R(\tau)=E[\xi(t)\xi(t+\tau)]$$

具有以下性质：

• $R(0)=E[\xi^2(t)]$，表示$\xi(t)$的平均功率，这在之后的维纳-辛钦定理中会有所体现。
• $R(-\tau)=R(\tau)$，表示自相关函数是偶函数
• $|R(\tau)|\leq R(0)$，表示自相关函数上界，在$\tau=0$时取得最大值。
• $R(\infty)=E^2[\xi(t)]$，表示$\xi(t)$的直流功率。
• $R(0)- R(\infty)$，表示$\xi(t)$的交流功率。

类似于功率信号，根据维纳-辛钦定理，平稳随机过程的功率谱密度$P_{\xi}(f)$与其相关函数$R(\tau)$也构成一对傅里叶变换对：

$$R(\tau) = \int_{-\infty}^{\infty}P_{\xi}(f)e^{j2\pi f\tau}df$$

3.2. 高斯随机过程

不同时刻不相关的高斯随机过程，其概率密度可简化为：

$$\begin{aligned} f_n(x_1,x_2,\cdots,x_n;t_1,t_2,\cdots,t_n)& =\prod_{k=1}^n\frac1{\sqrt{2\pi}\sigma_k}\mathrm{exp}\Big[-\frac{(x_k-a_k)^2}{2\sigma_k^2}\Big] \\ &=f(x_1,t_1)\cdot f(x_2,t_2)\cdot\cdots\cdot f(x_n,t_n) \end{aligned}$$

高斯分布或者高斯过程有个重要的性质为：经过线性变换仍为高斯。

3.3. 平稳随机过程通过线性系统

平稳随机过程通过线性系统，可以看作对于输入随机的所有样本进行线性变换后得到输出随机过程。
输出过程$\xi_o(t)$的统计特性为：

均值

$$E[\xi_o(t)]=E[\int_{-\infty}^{\infty}h(\tau)\xi_i(t-\tau)d\tau]= \int_{-\infty}^{\infty}h(\tau)E[\xi_i(t-\tau)]d\tau$$

因为输入随机过程为平稳的，则有$E[\xi_i(t-\tau)]=E[\xi_i(t)]=a$所以

$$E[\xi_o(t)]=a\int_{-\infty}^{\infty}h(\tau)d\tau=a \cdot H(0)$$

可以看出输出过程的均值也为常数，为输入过程的均值$a$乘以系统的直流分量。

自相关函数

$$\begin{aligned}R_{\mathrm{o}}(t_{1},t_{1}+\tau)&=E[\xi_{\mathrm{o}}(t_{1})\xi_{\mathrm{o}}(t_{1}+\tau)]\\&=E\left[\int_{-\infty}^\infty h(\alpha)\xi_i(t_1-\alpha)\mathrm{d}\alpha\int_{-\infty}^\infty h(\beta)\xi_i(t_1+\tau-\beta)\mathrm{d}\beta\right]\\&=\int_{-\infty}^\infty\int_{-\infty}^\infty h(\alpha)h(\beta)E[\xi_i(t_1-\alpha)\xi_i(t_1+\tau-\beta)]\mathrm{d}\alpha\mathrm{d}\beta\end{aligned}$$

因为输入过程为平稳的，所以有$E[\xi_i(t_1-\alpha)\xi_i(t_1+\tau-\beta)]=R_i(\tau+\alpha-\beta)$，所以有：

$$R_{\mathrm{o}}(t_{1},t_{1}+\tau)=\int_{-\infty}^\infty\int_{-\infty}^\infty h(\alpha)h(\beta)R_i(\tau+\alpha-\beta)\mathrm{d}\alpha\mathrm{d}\beta= R_o(\tau)$$

可以看出对于线性系统，如果输入过程为平稳的，则输出也为平稳。

功率谱密度

对于线性系统，其输出过程的功率谱密度$P_o(f)$与输入过程的功率谱密度$P_i(f)$之间的关系为：

$$\begin{aligned} P_{_0}(f) &= \int_{-\infty}^{\infty}R_{_0}( \tau ) \mathrm{e}^{-\mathrm{j}\omega\tau}\mathrm{d}\tau \\ &=\int_{-\infty}^{\infty}\left[\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}h\left(\alpha\right)h\left(\beta\right)R_{\mathrm{i}}\left(\tau+\alpha-\beta\right)\mathrm{d}\alpha\mathrm{d}\beta\right]\mathrm{e}^{-\mathrm{j}\omega\tau}\mathrm{d}\tau \\ &=\int_{-\infty}^{\infty}h\left(\alpha\right)\mathrm{e}^{\mathrm{j\omega\alpha}}\mathrm{d}\alpha\int_{-\infty}^{\infty}h\left(\beta\right)\mathrm{e}^{-\mathrm{j\omega\beta}}\mathrm{d}\beta\int_{-\infty}^{\infty}R_{\mathrm{i}}\left(\tau^{\prime}\right)\mathrm{e}^{-\mathrm{j\omega}\tau^{\prime}}\mathrm{d}\tau^{\prime}\\ &=H^*(f)\cdot H(f)\cdot P_{\mathrm{i}}(f)=|H(f)|^2P_{\mathrm{i}}(f) \end{aligned}$$

其中$H(f)$为系统的频率响应。

3.4. 窄带随机过程

若随机过程$\xi(t)$的谱密度集中在中心频率$f_c$附近，且带宽$B$远小于中心频率$f_c$，则称该随机过程为窄带随机过程，其可以表示为：

$$\xi(t)=a_{\xi}(t)cos[w_ct+\varphi_{\xi}(t)] \quad a_{\xi}(t) \geq 0$$

其中$a_{\xi}(t)$和$\varphi_{\xi}(t)$分别为窄带随机包络和窄带随机相位。
进行三角展可得：

$$\xi(t)= \xi_c(t)cos(w_ct)-\xi_s(t)sin(w_ct)$$

其中$\xi_c(t)=a_{\xi}cos\varphi_{\xi}(t)$和$\xi_s(t)=a_{\xi}sin\varphi_{\xi}(t)$分别为窄带随机过程的同相分量和正交分量。

3.4.1. $\xi_c(t)$ 和 $\xi_s(t)$的统计特性

均值

$$E[\xi(t)]=E[\xi_c(t)]\mathrm{cos}\omega_ct-E[\xi_s(t)]\mathrm{sin}\omega_ct$$

假设$\xi(t)$是一个均值为0，方差为$\sigma_{\xi}^2$的平稳高斯窄带随机过程，
因为$\xi(t)$平稳且均值为0，对于任意的时间$t$，其均值为$E[\xi(t)]=0$，所以有：

$$E[\xi_c(t)]=E[\xi_s(t)]=0$$

自相关函数

这里省去证明，对于自相关函数

$$\begin{aligned} R_c(\tau)&=R_s(\tau)\\ R_{cs}(\tau)&=-R_{sc}(\tau) \end{aligned}$$

因为互相关函数的性质可得：

$$R_{cs}(0)=R_{sc}(0)=0$$

一个均值为0的窄带高斯随机过程$\xi(t)$，他的同相分量$\xi_c(t)$和正交分量$\xi_s(t)$同样是平稳高斯随机过程，且均值为0，方差也相同，且在同一时刻相互独立

3.4.2. $a_{\xi}(t)$ 和 $\varphi_{\xi}(t)$的统计特性

$\xi_c(t)$和$\xi_s(t)$的联合概率分布：

$$f(\xi_\mathrm{c},\xi_\mathrm{s})=f(\xi_\mathrm{c})\cdot f(\xi_\mathrm{s})=\frac1{2\pi\sigma_\xi^2}\mathrm{exp}\Big[-\frac{\xi_\mathrm{c}^2+\xi_\mathrm{s}^2}{2\sigma_\xi^2}\Big]$$

由Jacobian matrix可得：

$$f(a_{\xi}(t),\varphi_{\xi}(t)) = f(\xi_\mathrm{c},\xi_\mathrm{s}) \cdot \left|\frac{\partial(\xi_c,\xi_s)}{\partial(a_\xi,\varphi_\xi)}\right|$$

对单一变量进行积分得到边缘分布，可得$a_{\xi}$的概率密度函数为：

$$\begin{aligned}f(a_{\xi})&=\int_{-\infty}^\infty f(a_\xi,\varphi_\xi)\mathrm{d}\varphi_\xi=\int_0^{2\pi}\frac{a_\xi}{2\pi\sigma_\xi^2}\mathrm{exp}\Big[-\frac{a_\xi^2}{2\sigma_\xi^2}\Big]\mathrm{d}\varphi_\xi\\&=\frac{a_\xi}{\sigma_\xi^2}\mathrm{exp}\Big[-\frac{a_\xi^2}{2\sigma_\xi^2}\Big]\quad a_\xi\geqslant0\end{aligned}$$

而$\varphi_{\xi}$为：

$$\begin{aligned}f(\varphi_{\xi})&=\int_{0}^{\infty}f(a_{\xi},\varphi_{\xi})\mathrm{d}a_{\xi}\\\\&=\frac{1}{2\pi}\int_{0}^{\infty}\frac{a_{\xi}}{\sigma_{\xi}^{2}}\mathrm{exp}\biggl(-\frac{a_{\xi}^{2}}{2\sigma_{\xi}^{2}}\biggr)\mathrm{d}a_{\xi}=\frac{1}{2\pi}\quad0\leq\varphi_{\xi}\leq2\pi\end{aligned}$$

可见一个均值为0的窄带高斯随机过程$\xi(t)$，其包络$a_{\xi}$为瑞利分布，相位$\varphi_{\xi}$为均匀分布，且两者相互独立因为其满足$f(a_{\xi},\varphi_{\xi})=f(a_{\xi})\cdot f(\varphi_{\xi})$

3.5. 正弦波加窄带高斯噪声

与计算窄带高斯随机过程类似，这里不再赘述，直接得出结论，对于正弦波加窄带高斯噪声：

$$\begin{aligned} r(t)&=Acos(w_ct+\theta)+n(t)\\ & =[Acos\theta+n_c(t)]cos(w_ct)-[Asin\theta+n_s(t)]sin(w_ct) \end{aligned}$$

令

$$\begin{aligned} z_c(t)&=Acos\theta+n_c(t)\\ z_s(t)&=Asin\theta+n_s(t) \end{aligned}$$

给定相位$\theta$，则有

$$f(z)=\frac z{\sigma_n^2}\mathrm{exp}\Big[-\frac1{2\sigma_n^2}(z^2+A^2)\Big]I_0\Big(\frac{Az}{\sigma_n^2}\Big)$$

该概率密度函数为广义瑞利分布，其中$I_0$为第一类零阶修正贝塞尔函数。

结论存在两种情况：
当信号很小，即$A\rightarrow0$时，包络$f(z)$趋近于瑞利分布，相位$\theta$趋近于均匀分布；
当信号很大，包络$f(z)$在$z\approx A$附近趋近于高斯分布，相位$\theta$集中在信号相位附近。