principles-of-communication-04

Info

本文为《通信原理》的读书笔记，对应《通信原理》（第七版）by 樊昌信的第四章，主要介绍信道模型以及信道特性。

1. 信道模型

按照不同方式，一般信道可分为以下几类：

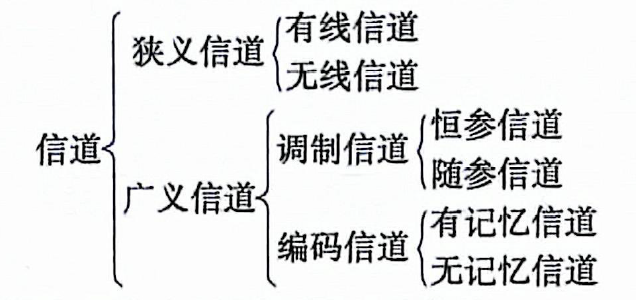
其中调制信道和编码信道都是为了研究通信系统中特定的module而视作的特殊信道：

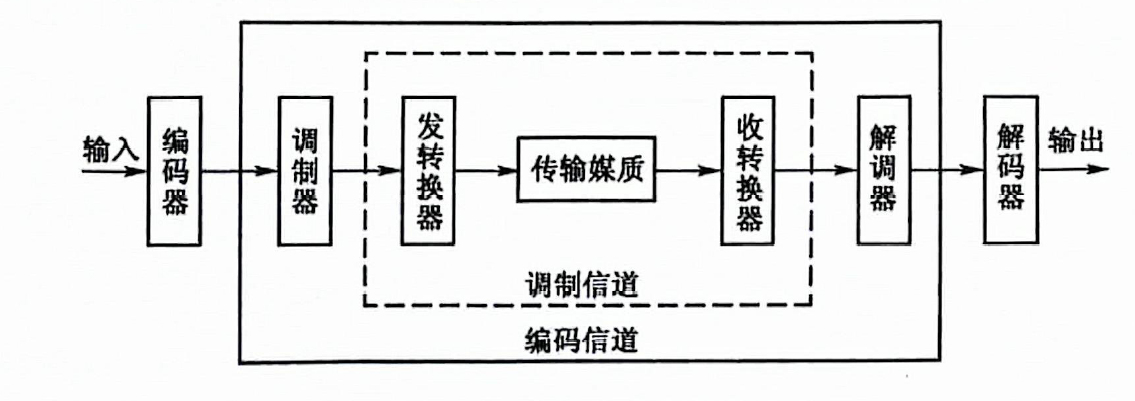
1.1. 恒参信道

恒参信道的传输特性可以用振幅频率特性和相位频率特性来描述。实际的信道可能不理想有两种失真：幅频失真和相频失真。两种失真都会让数字传输系统的产生码间串扰使误码率增大。这两种失真都为线性失真，可以通过线性网络补偿。这种网络为均衡器。

1.2. 随参信道

随参信道的传输特性是随时间变化的，其有三个主要特性：

• 信道的传输衰耗随时间变化
• 信道的传输时延随时间变化
• 多径传播

多径传播在无线信道中很常见，设发射信号为$Acos\omega t$，接收信号为$R(t)$可表示为：

$$\begin{aligned} R(t) & =\sum_{i=1}^n\mu_i(t)\mathrm{cos}\omega_0[t-\tau_i(t)]=\sum_{i=1}^n\mu_i(t)\mathrm{cos}[\omega_0t+\varphi_i(t)] \\ & = \sum_{i=1}^n\mu_i(t)\mathrm{cos}\varphi_i(t)\mathrm{cos}\omega_0t-\sum_{i=1}^n\mu_i(t)\mathrm{sin}\varphi_i(t)\mathrm{sin}\omega_0t \end{aligned}$$

其中$\mu_i(t)$表示第$i$路信号的幅度，$\tau_i(t)$为第$i$路信号的时延，这里的$\mu_i(t)$，$\tau_i(t)$和$\varphi_i(t)$都是随机变化的。

实验表明，与信号角频率$w_0$相比，信号的幅度和相位变化较慢，因此可认为接收信号$R(t)$可以看作两个互相正交的信号的组成：

$$\begin{aligned} R(t) &=\sum_{i=1}^n\mu_i(t)\mathrm{cos}\varphi_i(t)\mathrm{cos}\omega_0t-\sum_{i=1}^n\mu_i(t)\mathrm{sin}\varphi_i(t)\mathrm{sin}\omega_0t \\ & = X_c(t)\mathrm{cos}\omega_0t-X_s(t)\mathrm{sin}\omega_0t \\ & = Y(t)cos(\omega_0t+\varphi(t)) \end{aligned}$$

其中$V(t)= \sqrt{X_c^2(t)+X_s^2(t)}$为接收信号$R(t)$的包络。

和振幅恒定，单一频率的发射信号相比，接收信号有了扩展，频率不再单一，成了窄带信号。这种包络因传播有了变化称为衰落(fading)

假设两个多径信号的时间差为$\tau$，则接收信号为：

$$Af(t-\tau_0)+Af(t-\tau_0-\tau)\Leftrightarrow AF(\boldsymbol{\omega})\mathrm{e}^{-\mathrm{j}\boldsymbol{\omega}\tau_0}(1+\mathrm{e}^{-\mathrm{j}\boldsymbol{\omega}\tau})$$

$$H(\omega) = AF(\omega)e^{-j\omega\tau_0}(1+e^{-j\omega\tau})$$

其中与时延差有关的复因子模为：

$$|1+\mathrm{e}^{-\mathrm{j}\omega\tau}|=|1+\mathrm{cos}\omega\tau-\mathrm{j}\mathrm{sin}\omega\tau|=|\sqrt{\left(1+\mathrm{cos}\omega\tau\right)^2+\mathrm{sin}^2\omega\tau}|=2\left|\cos\frac{\omega\tau}2\right|$$

与$\tau$有关，这种衰落和频率有关，称为频率选择性衰落。如果信号带宽大于$\frac{1}{\tau}$，则信号中不同频率分量的幅度差异很大。将$\dfrac{1}{\tau}$称为相关带宽。

2. 信道噪声

为描述窄带噪声的带宽，引入噪声等效带宽$B_n$，定义为：

$$B_n = \dfrac{\int_{-\infty}^{\infty}P_n(f)\mathrm{d}f}{2P_n(f_0)} = \dfrac{\int_{0}^{\infty}P_n(f)\mathrm{d}f}{P_n(f_0)}$$

利用噪声等效带宽，认为窄带噪声的功率谱密度在带宽$B_n$内的功率为恒定的。

3. 信道容量

3.1. 离散信道容量

离散信道容量有两种不同的度量单位：一种是每个符号(symbol)所能传输的平均信息量最大值和用单位时间能传输的平均信息量最大值：$C$和$C_t$

从信息量的角度上看，离散信道容量为发射端对信源的不确定度减去接收端收到接收信号后对信源的不确定度：

$$C = H(X)-H(X|Y)$$

其中少的这部分$H(X|Y)$为信道传输的不确定度，即信道传输错误引起的损失。

每个符号传输的平均信息量和信源发射符号概率$P(x_i)$有关，定义信道容量为最大值:

$$C=\max_{P(x_i)}[H(X)-H(X|Y)] \quad (\text{bits/symbol})$$

考虑两个极端，当信道无噪声时，$H(X|Y)=0$，信道容量为$H(X)$；当信道有无穷大的噪声时，信道容量为0。

设单位时间信道传输的bit数为$r(bit/s)$，则信道每秒传输的平均信息量为：

$$R=r*C = r[H(X)-H(X|Y)] \quad (\text{bit/s})$$

求出$R$的最大值，得出容量$C_t$为：

$$C_t = \max_{P(x)}[r[H(X)-H(X|Y)]] \quad (\text{bit/s})$$

3.2. 连续信道容量

连续信道的容量也有两种不同的计算单位，这里只介绍按时间计算的单位。

对于带宽有限，平均功率有限的高斯白噪声连续信道，其容量为：

$$\begin{aligned} C_t &= B\log_2(1+\dfrac{S}{N}) \quad (\text{bit/s}) \\ & = B\log_2(1+\dfrac{S}{n_0B}) \quad (\text{bit/s}) \end{aligned}$$

上述的$\color{red}{C_t = B\log_2(1+\dfrac{S}{N})}$即为香农公式，说明信道容量受三要素影响：信道带宽$B$，信号功率$S$，信道的噪声功率谱密度$n_0$。

当信道带宽$B$趋近$\infty$时，可以证明信道容量$C_t$并不是趋于$\infty$：

$$\begin{aligned} C_t =\frac S{n_0}\frac{Bn_0}S\mathrm{log}_2\left(1+\frac S{n_0B}\right)=\frac S{n_0}\mathrm{log}_2\left(1+x\right)^{1/x} \end{aligned}$$

当$x= \dfrac{S}{n_0B} \to \infty$时，此时信道容量为：

$$\lim_{B\to\infty}C_t=\lim_{x\to0}\frac S{n_0}\mathrm{log}_2(1+x)^{1/x}=\frac S{n_0}\mathrm{log}_2\mathrm{e}\approx1.44\frac S{n_0}\quad\mathrm{(bit/s)}$$