principles-of-communication-06

Info

第五章为模拟调制系统，目前模拟系统已经不是主流，因此省略。
本文为《通信原理》的读书笔记，对应《通信原理》（第七版）by 樊昌信的第六章，主要介绍数字基带传输系统。

1. 数字基带信号及其频谱特性

1.1. 数字基带信号

数字基带信号的波形可以采用不同的形式，这里用$g(t)$表示，则数字基带信号可以表示为：

$$s(t) = \sum_{n=-\infty}^{\infty}a_ng(t-nT_B)$$

其中$a_n$为第$n$个码元对应的电平值；$T_B$为码元持续时间；$g(t)$为某种基础波形。
由于$a_n$为随机量，则$s(t)$基带信号为随机的脉冲序列：

$$s(t) = \sum_{n=-\infty}^{\infty}s_n(t)$$

1.2. 频谱特性

对于二进制随机脉冲序列$s(t) = \sum_{n=-\infty}^{\infty}s_n(t)$，其中$s_n(t)$可用概率分布表示为：

$$s_n(t)=\begin{cases}g_1(t-nT_{B})&\text{以概率}P\text{出现}\\\\g_2(t-nT_{B})&\text{以概率}(1-P)\text{出现}\end{cases}$$

为简单推导$s(t)$可分解稳态波$v(t)$和交变波$u(t)$的和。
稳态波$v(t)$为各个码元的平均值：

$$v(t)=\sum_{n=-\infty}^\infty\left[Pg_1(t-nT_B)+(1-P)g_2(t-nT_B)\right]=\sum_{n=-\infty}^\infty v_n(t)$$

根据求和关系交变波$u(t)$满足：

$$u(t)=s(t)-v(t)$$

由于$v(t)$是周期信号，可以展开得到其傅里叶级数，随即可求得稳态波$v(t)$的功率谱密度为：

$$P_v(f)=\sum_{m=-\infty}^\infty|f_B[PG_1(mf_B)+(1-P)G_2(mf_B)]|^2\delta(f-mf_B)$$

交变波$u(t)$的功率谱密度为：

$$P_u(f)=f_BP(1-P)\mid G_1(f)-G_2(f)\mid^2$$

交变波$u(t)$的功率谱密度$P_u(f)$是连续谱，它与$g_1(t)$和$g_2(t)$的频谱特性以及概率$P$有关。通常可以根据连续谱确定随机序列的带宽。

则随机序列$s(t)$的功率谱密度为：

$$\begin{aligned} P_{s}(f)& =P_{u}(f)+P_{v}(f)=f_{B}P(1-P)\mid G_{1}(f)-G_{2}(f)\mid^{2}+ \\ m &\sum_{m=-\infty}^{\infty}\mid f_{B}[PG_{1}(mf_{B})+(1-P)G_{2}(mf_{B})]\mid^{2}\delta(f-mf_{B}) \end{aligned}$$

式中，$G_1(f)$和$G_2(f)$分别为$g_1(t)$和$g_2(t)$的傅里叶变换，$f_B=1/T_B$为码元速率。

1.3. 传输码型选择原则

• 不含直流，低频分量少。含有直流和低频分量的单极性波形就不适合在低频传输特性差的信道中传输
• 主瓣宽度窄，占用频带少
• 含有丰富的定时信息

2. 数字基带传输系统

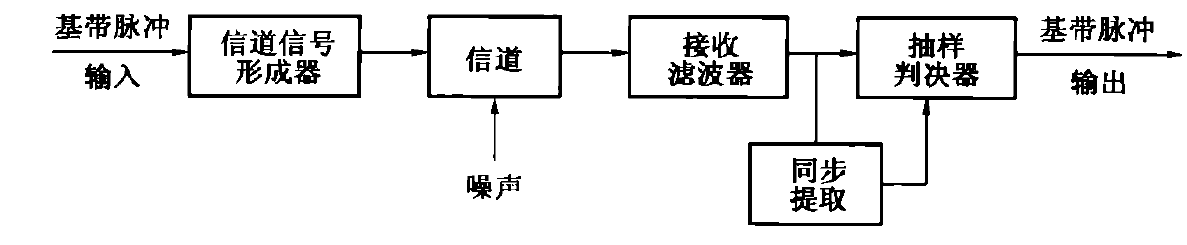
其数学模型为：

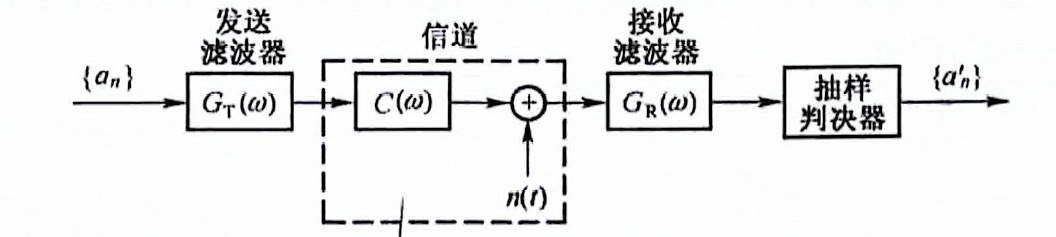
输入序列对应的数字基带信号为：

$$d(t)=\sum_{n=-\infty}^{\infty}a_{n}\delta(t-nT_{B})$$

基带传输系统的总传输特性为：

$$H(w) = G_T(w)C(w)G_R(w)$$

在冲激脉冲串序列$d(t)$经过基带传输系统后，输出信号为：

$$r(t)=d(t)*h(t)=\sum_{n=-\infty}^{\infty}a_{n}h(t-nT_{B})+ n_R(t)$$

然后抽样判决器对接收的信号$r(t)$进行抽样判决：

$$\begin{aligned}r( kT_{B} + t_{0} )&= a_{k}h( t_{0} ) + \sum_{n\neq k}a_{n}h[ ( k - n ) T_{B} + t_{0} ]\\&+ n_{H}( kT_{H} + t_{g} )\end{aligned}$$

式中，$t_0$为接收延迟，$a_kh(t_0)$为第$k$个码元的采样值，它是确定$a_k$的依据；$\sum_{n\neq k}a_{n}h[ ( k - n ) T_{B} + t_{0} ]$ 为除了第$k$个码元，其他所有码元波形在第$k$个抽样上的代数和。这个就是码间串扰值，其影响$a_k$的判决准确性。$n_H(kT_H+t_g)$为抽样判决器的输出噪声。

3. 无码间串扰的基带传输特性

3.1. 码间串扰

码间串扰是前面码元波形的拖尾影响到后面码元的采样值，导致判决错误，其主要原因是系统的总传输特性不理想，导致码元畸形、展宽。

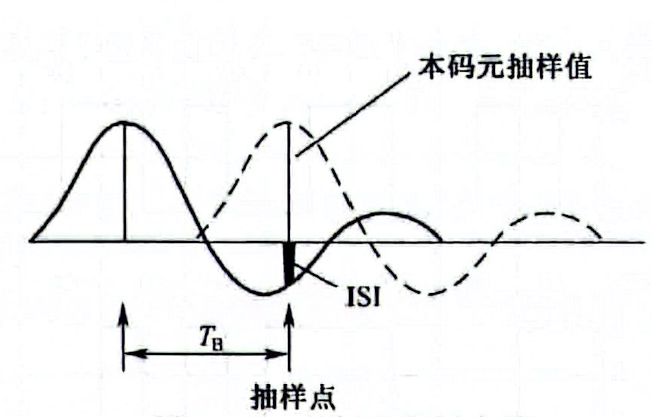
3.2. 无码间串扰条件

只要求其他码元的拖尾在特定采样时刻上取值为0，就可以消除码间串扰。

设时延为$t_0=0$，则要求系统相应满足：

$$h\left(kT_{B}\right) = \begin{cases}1&k = 0\\\\0&k \text{为其他整数}\end{cases}$$

上述时域形式的条件等价于频域条件：

$$\sum_iH(\omega+\frac{2\pi i}{T_B})=T_B\quad|\omega|\leq\frac\pi{T_B}$$

物理意义为：将$H(\omega)$的频谱以$2\pi i/T_B$的间隔隔开，然后分段沿$\omega$轴平移到$(-\dfrac{\pi}{T_B},\dfrac{\pi}{T_B})$频谱叠加，其幅度为常数。

3.3. 无码间串扰系统设计

3.3.1. 理想低通

满足上述$\sum_iH(\omega+\frac{2\pi i}{T_B})=T_B\quad|\omega|\leq\frac\pi{T_B}$条件的滤波器，很容易想到理想低通滤波器：

$$H(\omega) = \begin{cases}T_B&\quad| \omega | \leqslant\frac{\pi}{T_B}\\\\0&\quad| \omega | >\frac{\pi}{T_B}\end{cases}$$

其冲激响应（时域形式）为$h(t)=Sa(\pi t/T_B)$，很容易发现该时域形式的滤波器在$t=\pm kT_B$时有周期性零点满足无码间串扰的时域条件。

观察其频域易得带宽为$B=1/2T_B$，传输的波特率为$R_B=1/T_B$，频带利用率为$\eta=R_B/B=2$。

通常把理想传输特性的带宽成为奈奎斯特带宽，将该系统的无码间串扰的最高传输速率成为奈奎斯特速率。奈奎斯特带宽$f_N=1/2T_B(Hz)$，奈奎斯特速率$2f_N(\text{波特})$

不过该无码间串扰系统难以物理实现；并且冲激响应波形$h(t)$的衰减幅度较大；如果采样时间稍有偏差就会引起严重的码间串扰。

3.3.2. 余弦滚降

使理想低通滤波器特性的边沿缓慢下降，这成为 “滚降”，它要求$H(\omega)$在滚降段中心频率即奈奎斯特带宽$f_N$呈奇对称振幅特性，即可满足无码间串扰条件：

$$\begin{aligned}H(\omega)&=\begin{cases}T_B&0\leq|\omega|<\frac{(1-\alpha)\pi}{T_B}\\\\\frac{T_B}2\Big[1+\sin\frac{T_B}{2\alpha}\Big(\frac\pi{T_B}-\omega\Big)\Big]&\frac{(1-\alpha)\pi}{T_B}\leq|\omega|<\frac{(1+\alpha)\pi}{T_B}\\\\0&|\omega|\geq\frac{(1+\alpha)\pi}{T_B}\end{cases}\end{aligned}$$

对应时域形式为：

$$h\left(t\right)=\frac{\sin\pi t/T_B}{\pi t/T_B}\cdot\frac{\cos B\alpha\pi t/T_B}{1-4\alpha^2t^2/T_B^2}$$

式中$\alpha$为滚降系数，用于描述滚降程度：

$$\alpha = f_{\Delta}/f_{N}$$

式中$f_N$为奈奎斯特带宽；$f_\Delta$是奈奎斯特带宽的扩展量

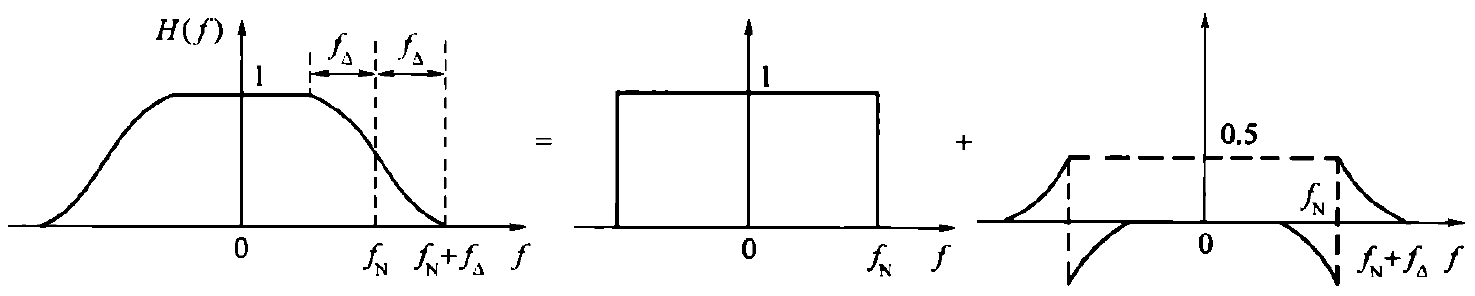
显然$0\leq\alpha\leq1$，不同的$\alpha$有不同的滚降特性，存在一个$tradeoff$：当$\alpha$越大，$h(t)$的拖尾衰减越快，对定时精度要求越低，但是带宽$B=f_N+f_\Delta = (1+\alpha)f_N$越大，频带利用率降低。当波特率取最大$2f_N$时，频带利用率为：

$$\eta=\frac{R_B}B=\frac{2f_\mathrm{N}}{(1+\alpha)f_\mathrm{N}}=\frac2{(1+\alpha)}\quad(\mathrm{~Baud/Hz})$$

根据公式容易看出：

• 当$\alpha=0$，传输特性为理想低通；
• 当$\alpha=1$，传输特性为全升余弦频谱特性

4. 无ISI基带传输系统的抗噪声能力

对于上述数字基带传输系统模型，信道加性噪声$n(t)$为平稳高斯白噪声，通过为线性网络的接受滤波器：

$$P_n(f) = \frac{n_0}{2}|G_R(f)|^2$$

4.1. 二进制双极性基带系统

这里省去证明，对于$P(1)=P(2)=\frac{1}{2}$，最佳的门限为：

$$V_\mathrm{d}^*=\frac{\sigma_n^2}{2A}{\ln\frac{P(0)}{P(1)}}=0$$

对于电平为$A$的双极性基带系统，其误码率为：

$$P_e=\frac12[P(0/1)+P(1/0)] =\frac12[1-\mathrm{erf}(\frac A{\sqrt{2}\sigma_n})]=\frac12\mathrm{erfc}(\frac A{\sqrt{2}\sigma_n})$$

在最佳门限下，二进制双极性基带系统的总误码率取决于信号峰值和均方根值的比值，而与采用什么样的信号形式无关

4.2. 二进制单极性基带系统

与双极性基带系统类似，其最佳门限变为：

$$V_\mathrm{d}^*=\frac{\sigma_n^2}{2A}{\ln\frac{P(0)}{P(1)}}+ \frac A2= \frac A2$$

其误码率为：

$$P_e=\frac12\mathrm{erfc}(\frac A{2\sqrt{2}\sigma_n})$$

对比双极性基带系统可以发现，在同样的$\dfrac A {\sigma_n}$条件下，双极性基带系统的抗噪性优于单极性系统。

5. 眼图

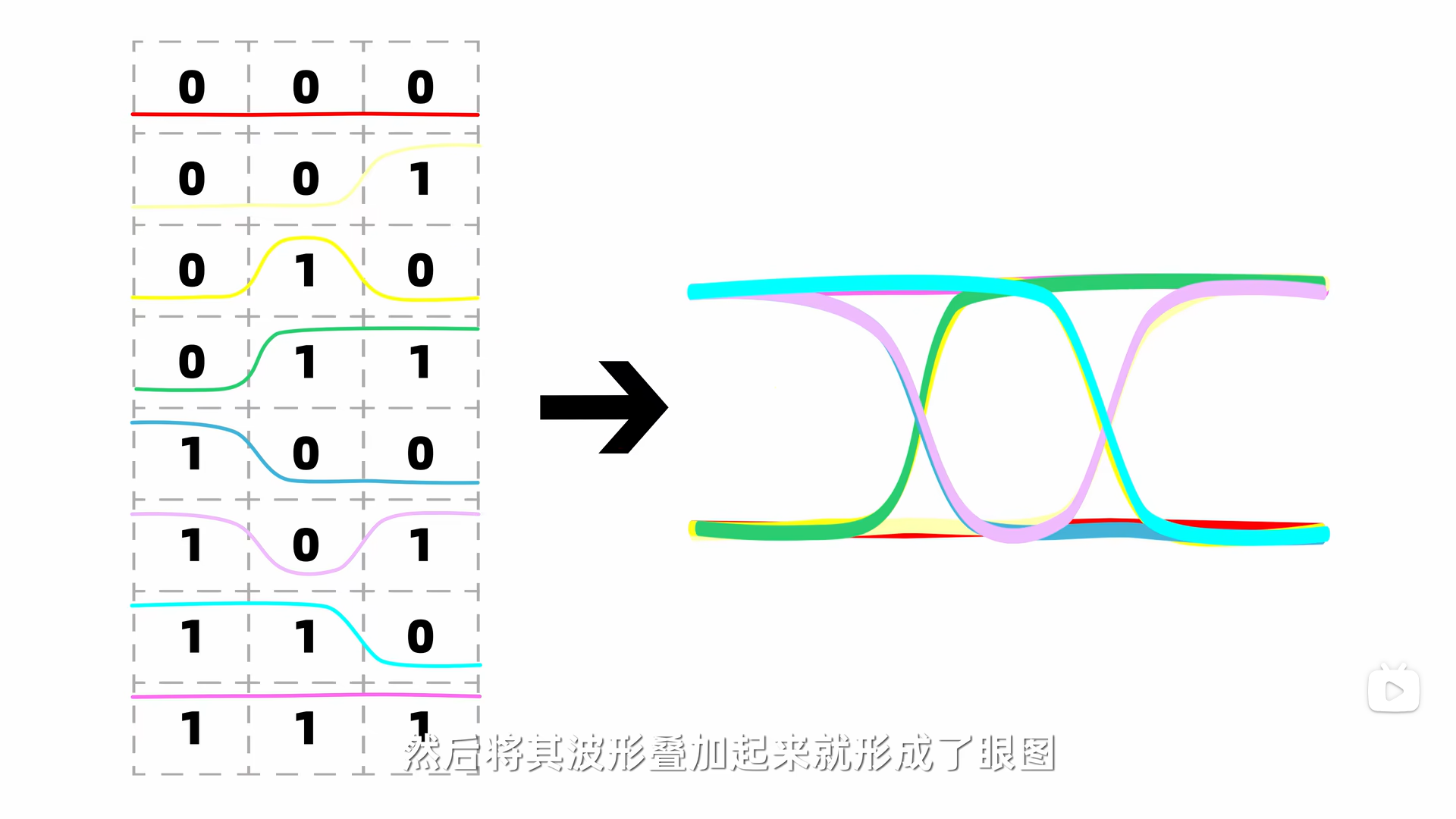
这里不做赘述，参考b站视频：BV1Cr4y1f7sm

6. 部分响应

部分相应技术既可以减少拖尾加快波形收敛，又可以提高频带利用率。

6.1. 第I类部分响应

可以将相距一个码元间隔的$sin(x)/x$波形叠加，使拖尾正负相加相互抵消：

$$\begin{aligned} g(t)&=\frac{\sin\frac\pi{T_B}\Big(t+\frac{T_B}2\Big)}{\frac\pi{T_B}\Big(t+\frac{T_B}2\Big)}+\frac{\sin\frac\pi{T_B}\Big(t-\frac{T_B}2\Big)}{\frac\pi{T_B}\Big(t-\frac{T_B}2\Big)}\\ & =\frac4\pi{\left(\frac{\cos\pi t/T_B}{1-4t^2/T_B^2}\right)} \end{aligned}$$

由公式可见，旁瓣是随着$t^2$程度下降的，相比原来$\dfrac {sin(x)}x$收敛速度快。

当码元速率为$1/T_B$时，在抽样时刻，仅与前一个码元形成码间干扰，这种串扰可以通过迭代的方式消除。

$$C_k=a_k+a_{k-1}$$

该编码形式成为相关编码，其实部分响应信号的必要形式，但是会带来差错传播问题。可采用预编码的方式解决，变为预编码-相关编码-模2的形式。

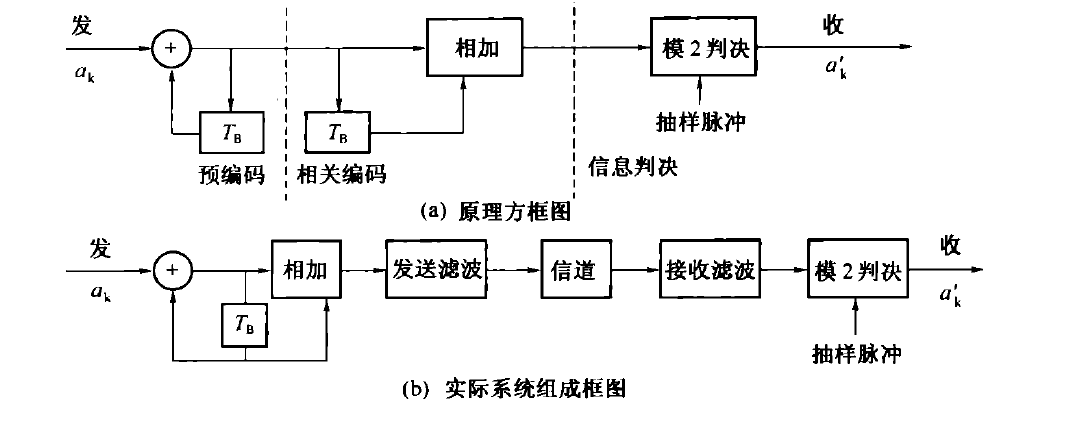
6.2. 部分响应一般形式

$$g(t)=R_1\frac{\sin\frac\pi{T_B}t}{\frac\pi{T_B}t}+R_2\frac{\sin\frac\pi{T_B}(t-T_B)}{\frac\pi{T_B}(t-T_B)}+\cdots+R_N\frac{\sin\frac\pi{T_B}[t-(N-1)T_B]}{\frac\pi{T_B}[t-(N-1)T_B]}$$

其中，$R_1,R_2,\cdots,R_{N-1}$为部分响应波形的加权系数和，当$R_1=R_2=1,R_m=0(m>2)$时，部分响应波形为第I类部分响应波形。
其接收电平为：

$$C_k=R_1a_k+R_2a_{k-1}+\cdots+R_Na_{k-(N-1)}$$

一般的部分相应也可以通过预编码-相关编码-模2的形式避免相关编码带来的差错传播问题。

7. 均衡

由于在通信系统实际实现时，滤波器设计误差和信道特性变化，总会在抽样时刻存在码间串扰，可使用
均衡减小码间串扰。
其中频率均衡在信道特性不变，传输低速数据可以使用，而时域均衡可以根据信道特性变化进行调整，有效减小码间串扰。

7.1. 时域均衡原理

无码间串扰的频域形式要求：$\sum_iH(\omega+\frac{2\pi i}{T_B})=\text{constent}\quad|\omega|\leq\frac\pi{T_B}$可以使用插入滤波器$T(\omega)$使得$H^{\prime}(\omega)=T(\omega)H(\omega)$满足上述公式，若$T(\omega)$以$\dfrac{2\pi i}{T_B}$为周期，则有：

$$T(\omega)=\frac{T_\mathrm{B}}{\sum_iH(\omega+\frac{2\pi i}{T_\mathrm{B}})}\quad|\omega|\leq\frac\pi{T_\mathrm{B}}$$

对于周期信号$h_T(t)$，可用傅里叶级数表示：

$$\begin{aligned} C_n&=\frac{T_\mathrm{B}}{2\pi}\int_{-\pi/T_\mathrm{B}}^{\pi/T_\mathrm{B}}T(\omega)\mathrm{e}^{\mathrm{j}n\omega T_\mathrm{B}}\mathrm{d}\omega \\ &=\frac{T_B}{2\pi}\int_{-\pi/T_B}^{\pi/T_B}\frac{T_B}{\sum_iH\left(\omega+\frac{2\pi i}{T_B}\right)}\mathrm{e}^{\mathrm{j}n\omega T_B}\mathrm{d}\omega \end{aligned}$$

可以发现均衡器的傅里叶级数只和原系统响应$H(\omega)$有关，对其进行傅里叶反变换，可得到称为横向滤波器的可调滤波器的冲激响应：

$$h_T(t)=F^{-1}\left[T(\omega)\right]=\sum_{n=-\infty}^\infty C_n\delta(t-nT_B)$$

可以通过横向排列的抽头和延迟单元实现上述网络：

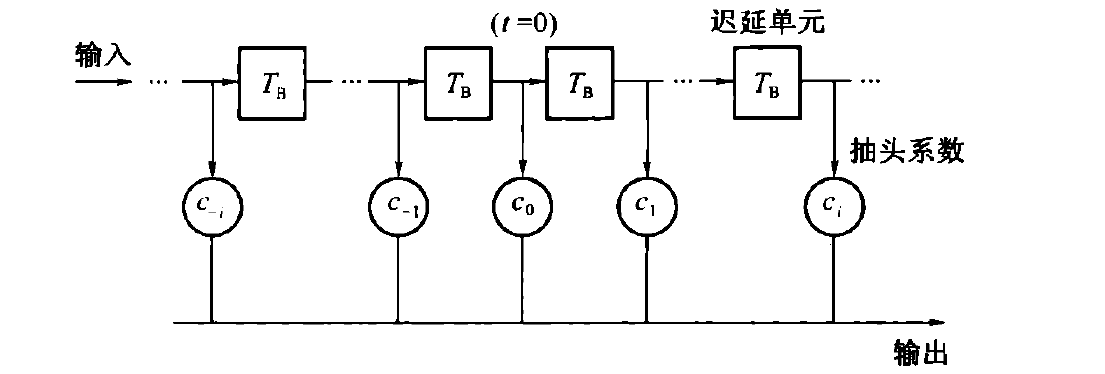
当抽头个数以及相应的可调系数无穷多，该横向滤波器可以完全消除抽样时刻上的码间串扰，但在实际中不存在，需要考虑有限长的横向滤波器。有限长的横向滤波器不能实现所有的$y(t)=x(t)*e(t)=\sum_{i=-N}^NC_ix(t-iT_B)$在$t=kT_B$时的零值。度量失真的指标为：

• 峰值失真：$D=\frac{1}{y_0} \sum_{\substack{k=-\infty \\ k \neq 0}}^{\infty}\left|y_k\right|$
• 均方失真：$e^2=\frac{1}{y_0^2} \sum_{\substack{k=-\infty \\ k \neq 0}}^{\infty} y_k^2$