principles-of-communication-08

Info

本文为《通信原理》的读书笔记，对应《通信原理》（第七版）by 樊昌信的第八章，主要介绍新型数字调制技术，如QAM，OFDM等。

1. 正交振幅调制QAM

前面提到的多进制键控调制方式，PSK调制方式在带宽和功率方面都具有优势，即带宽占用小和信噪比要求低，因此PSK调制方式多被使用。但是随之进制M的增大，MPSK的噪声容限性能会逐渐下降，因此需要引入新的调制方式，正交振幅调制QAM方式就是其中一种。

1.1. 信号表示

QAM调制体制码元表示方式：

$$\begin{aligned} e_k(t)&=A_k\mathrm{cos}(\omega_\mathrm{c}t+\theta_k)\quad kT_\mathrm{B}\leq t\leq(k+1)T_\mathrm{B} \\ &=A_k\mathrm{cos}\theta_k\mathrm{cos}\omega_ct-A_k\mathrm{sin}\theta_k\mathrm{sin}\omega_ct \\ &=X_k\mathrm{cos}\omega_\mathrm{c}t+Y_k\mathrm{sin}\omega_\mathrm{c}t \end{aligned}$$

其中，$X_k=A_k\mathrm{cos}\theta_k$，$Y_k=-A_k\mathrm{sin}\theta_k$，$A_k$为振幅，$\theta_k$为相位，$T_\mathrm{B}$为码元持续时间，$\omega_\mathrm{c}$为载波频率。公式可以看出QAM调制信号可以看作两个正交的振幅键控信号和。

1.2. 星座图

信号矢量端点的分布图称为星座图，可以用来描述QAM调制的信号空间分布状态。星座图的坐标轴分别为两个正交的基函数，星座图的点表示不同的码元。MQAM的星座图如下：

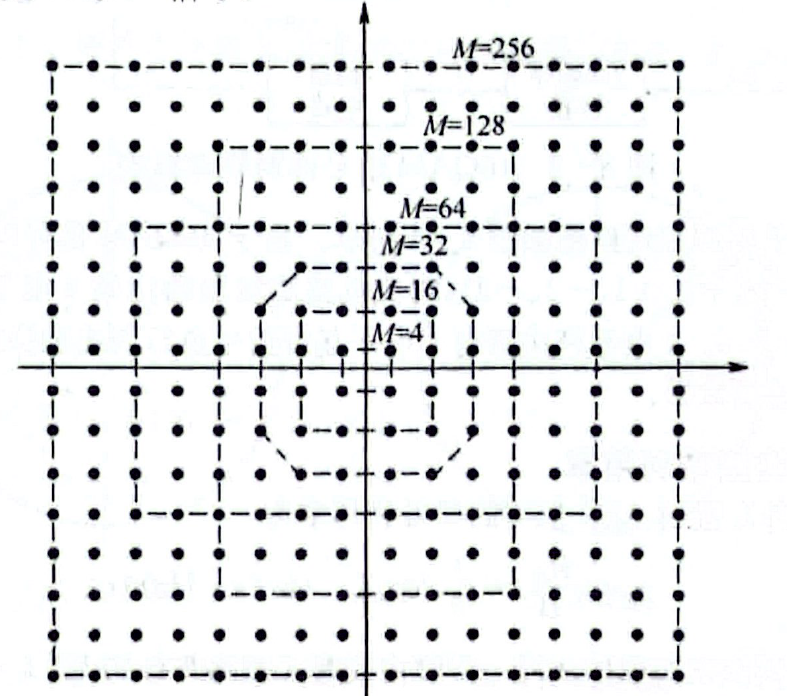
方型MQAM信号可以用两路正交的$\sqrt{M}$进制的ASK信号叠加而形成。

1.3. 带宽和频带利用率

上一章分析，单路$L$进制ASk信号的频带利用率为：

$$\eta_{\mathrm{b}}=\frac{R_{\mathrm{b}}}{B}=\frac{1}{2}\log_{2}L\quad\mathrm{(b/(s\cdot Hz))}$$

而QAM信号是两路正交的$\sqrt{M}$进制ASK信号叠加而成，因此QAM信号的频带利用率为：

$$\eta_{\mathrm{MQAM}}=2\times\frac{1}{2} \log_{2}L=\frac{1}{2} \log_{2}L^{2}=\frac{1}{2} \log_{2}M\quad\mathrm{(b/(s\cdot Hz))}$$

2. 最小频移键控MSK

MSK是2FSK的改进型，是一种包络恒定、相位连续、带宽最小且严格正交的2FSK信号。

2.1. 正交2FSK信号的最小频率间隔

理论上要求，如果两个信号相互正交，就可以在接收端将两个信号分开，假设2FSk发射信号的表达式为：

$$e(t)=\begin{cases}A\cos(\omega_1t+\varphi_1)&\text{发送“1”时}\\\\A\cos(\omega_0t+\varphi_0)&\text{发送“0”时}&\end{cases}$$

满足正交条件：

$$\int_0^{T_B}[\cos(\omega_1t+\varphi_1)\cdot\cos(\omega_0t+\varphi_0)]\mathrm{d}t=0$$

近似可得，$(\omega_1-\omega_0)T_\text{B}=2m\pi$，其中$Qm$为整数，当$m=1$时，

$$f_1-f_0=\frac{1}{T_\text{B}}$$

即最小频率间隔为$\frac{1}{T_\text{B}}$。

上述讨论的初始相位$\varphi_1$和$\varphi_0$是任意的，所以只能采用非相干剑波器接收（相干检波需要接收器产生同频同相的相干波，否则低频滤波器的输出会有$cos(\varphi)$的衰减因子），对于相干检波，初始相位是确定的，不妨设$\varphi_1-\varphi_0=0$，则有：

$$\sin(\omega_1-\omega_0)T_B=0$$

所以对于相干接收，最小频率间隔为$\dfrac{1}{2T_B}$。

2.2. MSK基本原理

MSK码元的表达式为：

$$e_{\mathrm{MSK}}(t)=\cos\left[\omega_{\mathrm{c}}t+\theta_{k}(t)\right]=\cos\left[\omega_{\mathrm{c}}t+\frac{a_{k}\pi}{2T_{\mathrm{B}}}t+\varphi_{k}\right]\quad kT_{\mathrm{B}}\leqslant t\leqslant(k+1)T_{\mathrm{B}}$$

其中，$a_k$为发送符号，$\theta_k(t)$为相位，$\varphi_k$为初始相位，$T_{\mathrm{B}}$为码元宽度，$\omega_{\mathrm{c}}$为载波频率，$\dfrac{a_{k}\pi}{2T_{\mathrm{B}}}$为相对于$\omega_{\mathrm{c}}$的频率偏移。

3. 正交频分复用OFDM

OFDM是一种多载波调制技术，通过将高速数据流分割成多个低速数据流，然后在不同的载波上进行调制，从而提高系统的频谱利用率。

OFDM的缺点主要有两个：

• 对信道产生的频率偏移和相位噪声很敏感；
• 信号峰值功率和平均功率的比值较大，这将会降低射频功率放大器的效率。

3.1. OFDM基本原理

对于一个有$N$个子载波的OFDM系统，每个子信道子载波为：

$$x_k(t)=B_k\cos(2\pi f_kt+\varphi_k)=0,1,\cdots,N-1$$

其中$B_k$为子载波的振幅，$f_k$为子载波的频率，$\varphi_k$为子载波的相位。

则子载波的和为：

$$e(t)=\sum_{k=0}^{N-1}x_k(t)=\sum_{k=0}^{N-1}B_k\cos(2\pi f_kt+\varphi_k)$$

写成复数为：

$$e(t)=\sum_{k=0}^{N-1} \boldsymbol{B}_k \mathrm{e}^{\mathrm{j}(2\pi f_kt+\varphi_k)}$$

我们希望等式右边为不含虚部，输入的复数据$\boldsymbol{B}_k$应满足某种条件。

为了使这$N$路子信道信号在接收时能够完全分离，要求它们满足正交条件。在码元持续时间$T_B$：内任意两个子载波都正交的条件为：

$$\int_0^{T_B}\cos(2\pi f_kt+\varphi_k)\cos(2\pi f_it+\varphi_i)\mathrm{d}t=0$$

满足上述条件的子载波频率$f_k$为：

$$f_k=(m+n)/2T_B,\quad f_i=(m-n)/2T_B$$

既要求子载波载频：

$$f_k=k/2T_B$$

且要求最小子载波间隔为：

$$\Delta f_{\min}=1/T_B$$

虽然OFDM系统的子载波的频率是有相互交叠的但是因为它们之间是相互正交的所以仍能在接收端相互分离，能够充分利用频带。并且根据划分的子信道的特点可以使用相应具有优势的调制技术

设一OFDM系统中共有$N$路子载波，子信道码元持续时间为$T_B$，每路子载波均采用$M$进制的调制，则它占用的频带宽度为：

$$B_{\mathrm{OFDM}}=\frac{N+1}{T_{\mathrm{B}}}\quad\mathrm{(Hz)}$$

频带利用率为单位带宽传输的比特率：

$$\eta_{\mathrm{b/OFDM}}=\frac{N\mathrm{log}_2M}{T_\mathrm{B}}\cdot\frac1{B_\mathrm{OFDM}}=\frac N{N+1}\mathrm{log}_2M\quad\mathrm{(b/(s\cdot Hz))}$$

当$N$很大时，$\eta_{\mathrm{b/OFDM}}$接近$\mathrm{log}_2M$

若用单个载波的$M$进制码元传输，为得到相同的传输速率，则码元持续时间应缩短为$T_B/N$，而占用带宽等于$2N/T_B$：，故频带利用率为：

$$\eta_{\mathrm{h}/M}=\frac{N\mathrm{log}_2M}{T_\mathrm{B}}\cdot\frac{T_\mathrm{B}}{2N}=\frac12\mathrm{log}_2M\quad\mathrm{(b/(s\cdot Hz))}$$

可见OFDM体制的调制和串行的单载波体制相比，频带利用率增大了一倍。

3.2. OFDM的实现

再度观察复数形式的OFDM信号表达形式：

$$e(t)=\sum_{k=0}^{N-1} \boldsymbol{B}_k \mathrm{e}^{\mathrm{j}(2\pi f_kt+\varphi_k)}$$

可以看出OFDM信号是由$N$个正交的子载波信号叠加而成，因此可以采用IDFT和FFT技术来实现OFDM信号的调制和解调。