principles-of-communication-09

Info

本文为《通信原理》的读书笔记，对应《通信原理》（第七版）by 樊昌信的第九章，主要介绍数字信号的最佳接收，包括最佳接受准则、匹配滤波器等，关于通信原理的重点章节已经完成，这篇暂且是《通信原理》的最后一章笔记，接下来按读书计划为Digital communications 5th by John G. Proakis

1. 数字信号的最佳接收

对于$M$进制的数字通信系统，只考虑噪声影响即$r(t)=s(t)+n(t)$，当发送码元是$s_i(t)$时，接收到的码元为：

$$f_i(r)=\frac1{(\sqrt{2\pi}\sigma_n)^k}\mathrm{exp}\Big\{-\frac1{n_0}\int_0^{T_B}\Big[r(t)-s_i(t)\Big]^2\mathrm{d}t\Big\}$$

数字通信系统的总误码率为：

$$\begin{aligned} P_{\mathrm{e}}&=P(1)P_{\mathrm{e}1}+P(0)P_{\mathrm{e}0}\\ &=P(1)\int_{A_0}f_1(r)\mathrm{d}r+P(0)\int_{A_1}f_0(r)\mathrm{d}r \end{aligned}$$

假设系统为简单的二进制传输数字系统，则：

$$P_e=P(1)\int_{-\infty}^{r_0^{\prime}}f_1(r)\mathrm{d}r+P(0)\int_{r_0^{\prime}}^{\infty}f_0(r)\mathrm{d}r$$

令偏导数为零可得，最佳的判决分界点：

$$\frac{P(1)}{P(0)}=\frac{f_0(r_0)}{f_1(r_0)}$$

2. 确知信号最佳接收机

2.1. 确知信号最佳接受准则

之前提到加噪后接收码元的的概率密度表达形式代入接受准则，可得：

$$n_{0}\ln\frac{1}{P(1)} + \int_{0}^{T_{\mathrm{B}}} \left[r(t) - s_{1}(t)\right]^{2} \, \mathrm{d}t > n_{0}\ln\frac{1}{P(0)} + \int_{0}^{T_{\mathrm{B}}} \left[r(t) - s_{0}(t)\right]^{2} \, \mathrm{d}t$$

假设波形的能量相同$\int_0^{T_B}s_0^2\left(t\right)\mathrm{d}t=\int_0^{T_B}s_1^2\left(t\right)\mathrm{d}t$，化简得：

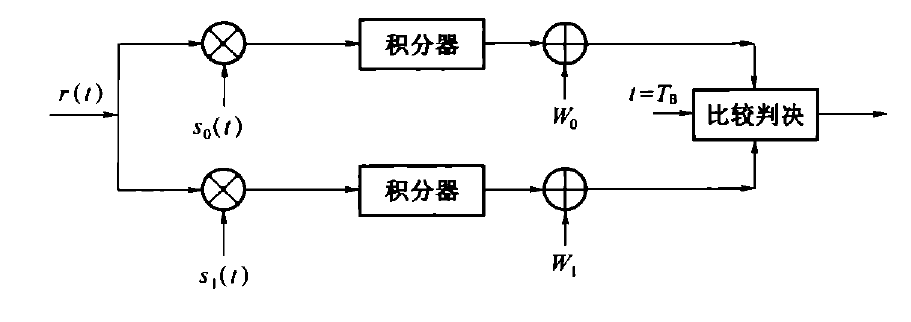
$$W_1+\int_0^{T_B}r(t)s_1(t)\mathrm{d}t<W_0+\int_0^{T_B}r(t)s_0(t)\mathrm{d}t$$

式子中，$W_0 = \dfrac{n_0}{2}\mathrm{ln}P(0)$, $W_1= \dfrac{n_0}{2}\mathrm{ln}P(1)$

若先验概率$P(1)=P(0)=0.5$，则最佳接收机的判决准则可进一步简化为：

$$\int_0^{T_B}r(t)s_1(t)\mathrm{d}t<\int_0^{T_B}r(t)s_0(t)\mathrm{d}t$$

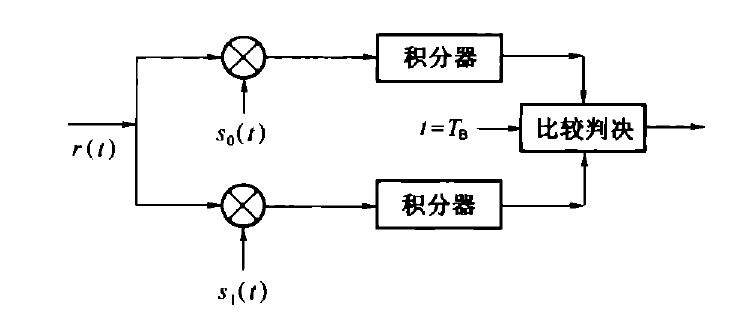
此时系统框图不需要先验概率的加权：

2.2. 确知信号最佳接受的误码率

在先验概率相等的情况下，这里省去证明，二进制确知信号的最佳接收机的误码率为：

$$P_{\mathrm{e}}=\frac{1}{\sqrt{2\pi}}\int_{A}^{\infty}\exp\Bigl(-\frac{x^{2}}{2}\Bigr) \mathrm{d}x=\frac{1}{2}\mathrm{erfc}\Bigl(\frac{A}{\sqrt{2}}\Bigr)$$

其中，$A=\sqrt{\frac{1}{2n_{0}}\int_{0}^{T_{\mathrm{B}}}[s_{0}(t)-s_{1}(t)]^{2}\mathrm{d}t}$

上式表明，误码率与信号能量之差$[s_{0}(t)-s_{1}(t)]^{2}$有关，而与波形形状无关，波形能量差异越大，$A$越大，误码率越小。

为此引入形容波形间的互相关系数：

$$\rho=\frac{\int_0^{T_\mathrm{B}}s_0\left(t\right)s_1\left(t\right)\mathrm{d}t}{\sqrt{E_0E_1}}$$

其中，$E_0=\int_0^{T_\mathrm{B}}s_0^2\left(t\right)\mathrm{d}t$，$E_1=\int_0^{T_\mathrm{B}}s_1^2\left(t\right)\mathrm{d}t$为两波形的能量。当$E_0=E_1=E_b$时：

$$P_{\mathrm{e}}=\frac{1}{2}\mathrm{erfc}\biggl[\sqrt{\frac{E_{\mathrm{b}}(1-\rho)}{2n_{0}}}\biggr]$$

对于二进制数字信号系统：

• 当$\rho=1$时，此时两波形相同，$P_{\mathrm{e}}=\dfrac 12$；性能最差，接收机在物理上为瞎猜
• 当$\rho=0$时，此时两波形正交（如2FSK），$P_{\mathrm{e}}=\dfrac 12\mathrm{erfc}\biggl(\sqrt{\dfrac{E_{\mathrm{b}}}{2n_{0}}}\biggr)$；性能最佳
• 当$\rho=-1$时，此时两波形相反，$P_{\mathrm{e}}=\dfrac 12\mathrm{erfc}\biggl(\sqrt{\dfrac{E_{\mathrm{b}}}{n_{0}}}\biggr)$

误码率仅和$E_b/n_0$,以及相关系数$\rho$有关，与信号波形和噪声功率没有直接关系，码元能量$E_b$和噪声功率谱密度$n_0$之比在系统带宽刚好等于$1/T_B$时是等于信噪比的：

$$\frac{E_\mathrm{b}}{n_0}=\frac{P_\mathrm{s}T_\mathrm{B}}{n_0}=\frac{P_\mathrm{s}}{n_0(1/T_\mathrm{B})}=\frac{P_\mathrm{s}}{n_0B}=\frac{P_\mathrm{s}}{P_\mathrm{n}}$$

实际上的通信系统，并不能满足$\dfrac{E_\mathrm{b}}{n_0}$就等于信号噪声功率比。因此实际接收机的性能总比最佳接受机的性能差：

3. 匹配滤波接收

上边讲述了将错误概率最小作为的最佳接受准则，其中误码率和信噪比相关，而匹配滤波器是一种能在特定时刻获得最大输出信噪比的最佳线性滤波器。

设接受滤波器的系统函数为$H(f)$，码元$s(t)$持续时间为$T_B$，则加噪后的信号为：

$$r(t)=s(t)+n(t)\quad 0\leq t\leq T_{\mathrm{B}}$$

根据随机信号输入系统的功率谱密度，易得在抽样时刻$t_0$的信号瞬时功率和噪声平均功率之比为：

$$r_0=\frac{|s_{\mathrm{oy}}(t_0)|^2}{N_0}=\frac{\left|\int_{-\infty}^\infty H(f)S(f)\mathrm{e}^{\mathrm{j}2\pi ft_0}\mathrm{d}f\right|^2}{\frac{n_0}2\int_{-\infty}^\infty|H(f)|^2\mathrm{d}f}$$

由施瓦兹不等式可得：

$$r_{0}\leq\frac{\int_{-\infty}^{\infty}|H(f)|^{2}\mathrm{d}f\int_{-\infty}^{\infty}|S(f)|^{2}\mathrm{d}f}{\frac{n_{0}}{2}\int_{-\infty}^{\infty}|H(f)|^{2}\mathrm{d}f}=\frac{\int_{-\infty}^{\infty}|S(f)|^{2}\mathrm{d}f}{\frac{n_{0}}{2}}=\frac{2E}{n_{0}}$$

其中$E=\int_{-\infty}^{\infty}|S(f)|^{2}\mathrm{d}f$为信号码元的能量。
当$H(f)=kS^*\left(f\right)\mathrm{e}^{-\mathrm{j}2\pi ft_0}$等号成立，即得到最大的输出信噪比$2E/n_0$

匹配滤波器的时域形式：

$$\begin{aligned} h(t)& =\int_{-\infty}^{\infty}H(f) \mathrm{e}^{\mathrm{j}2\pi ft} \mathrm{d}f = \int_{-\infty}^{\infty}kS^*\left(f\right)\mathrm{e}^{-\mathrm{j}2\pi fi_{0}}\mathrm{e}^{\mathrm{j}2\pi ft}\mathrm{d}f \\ &=k\int_{-\infty}^{\infty}\left[\int_{-\infty}^{\infty}s(\tau)\mathrm{e}^{-\mathrm{j}2\pi f\tau}\mathrm{d}\tau\right]^*\mathrm{e}^{-\mathrm{j}2\pi f(t_0-t)}\mathrm{d}f \\ &=k\int_{-\infty}^\infty\left[\int_{-\infty}^\infty\mathrm{e}^{j2\pi f(\tau-t_0+t)}\mathrm{d}f\right]s\left(\tau\right)\mathrm{d}\tau \\ &=k\int_{-\infty}^\infty s(\tau)\delta(\tau-t_0+t)\mathrm{d}\tau=ks(t_0-t) \end{aligned}$$

可见，$h(t)$是输人信号$s(t)$的镜像$s(-t)$，并延时$t_0$。

对于物理可实现的匹配滤波器，应有$s(t)=0,\quad t>t_{0}$，这表示$s(t)$必须在最大输出信噪比时刻之前结束。换言之，$t_0$应不小于$s(t)$的持续时间（即终止时刻）$T$，即$t_o\geq T$。一般取$t_0=T$，这意味着每个码元的终止时刻即为最佳抽样时刻。

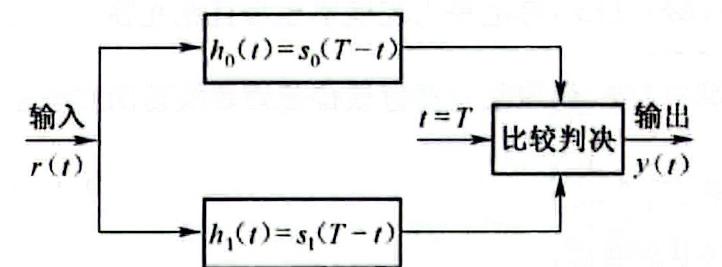
对于二进制数字传输系统，使用匹配滤波器的最佳接收机框图：

4. 最佳基带传输系统

最佳接收机只是接收系统的最佳化，而不是整个通信系统的最佳化。而数字基带传输系统最佳化的设计目标是：无码间串扰且误码率最小。
基带传输系统的总传输特性为：

$$H(w) = G_T(w)C(w)G_R(w)$$

为消除码间串扰，我们只考虑了信号传输函数，没有考虑信道的加性噪声。需要考虑既满足消除码间串扰，同时误码率最小的系统，这样的基带传输系统称为最佳基带传输系统。

4.1. 理想信道的最佳基带传输系统

理想信道指的是信号传输函数$C(\omega)=1$，此时设计

$$G_{\mathrm{T}}(\omega)=G_{\mathrm{R}}(\omega)=H^{1/2}(\omega)$$

则可得到一个既能消除码间串扰，同时又有最好的抗噪声性能的最佳基带系统。

4.2. 非理想信道的最佳基带传输系统

此时接受机得到的码元频谱为$G_T(f)\cdot C(f)$，在接收端采用匹配滤波器：

$$G_{\mathrm{R}}^{\prime}(f)=G_{\mathrm{T}}^{\star}(f)\cdot C^{\star}(f)$$

这时，基带传输系统的总传输特性为：

$$\begin{aligned} H(f) &= G_{\mathrm{T}}(f) \cdot C(f) \cdot G_{\mathrm{R}}^{\prime}(f) \\ &= G_{\mathrm{T}}(f) \cdot C(f) \cdot G_{\mathrm{T}}^{*}(f) \cdot C^{*}(f) \\ &= \left| G_{\mathrm{T}}(f) \right|^{2} \left| C(f) \right|^{2} \end{aligned}$$

为了消除码间串扰，由第6章的讨论得知，$H(f)$必须满足：

$$\sum_iH\left(\omega+\frac{2\pi i}{T_B}\right)=T_B\quad|\omega|\leqslant\frac{\pi}{T_B}$$

因此还需要增加均衡滤波器$T(f)$：

$$T(\omega)=\frac{T_{\mathrm{B}}}{\sum_{i} \left|G_{\mathrm{T}}(\omega+\frac{2\pi i}{T_{\mathrm{B}}})\right|^{2} \left|C(\omega+\frac{2\pi i}{T_{\mathrm{B}}})\right|^{2}}\quad| \omega|\leqslant\frac{\pi}{T_{\mathrm{B}}}$$